If you find Complexity Thoughts interesting, follow us! Click on the Like button, leave a comment, repost on Substack or share this post. It is the only feedback I can have for this free service. The frequency and quality of this newsletter relies on social interactions. Thank you!
Foundations of network science and complex systems
Beyond Linear Response: Equivalence between Thermodynamic Geometry and Optimal Transport
Thermodynamic geometry is an approach based on differential geometry to study thermodynamic systems. It maps thermodynamic quantities, such as temperature, pressure and entropy in a geometric space where the properties of the system can be explored through geometric structures like metrics and curvature (we use similar tricks in the different flavors of network geometry).
In a nutshell, the thermodynamic state space is endowed with a Riemannian metric (often derived from the Hessian of a thermodynamic potential), and the curvature of this space provides insights into the system’s properties, such as phase transitions, stability, and critical behavior.
A fundamental result of thermodynamic geometry is that the optimal, minimal-work protocol that drives a nonequilibrium system between two thermodynamic states in the slow-driving limit is given by a geodesic of the friction tensor, a Riemannian metric defined on control space. For overdamped dynamics in arbitrary dimensions, we demonstrate that thermodynamic geometry is equivalent to 𝐿2 optimal transport geometry defined on the space of equilibrium distributions corresponding to the control parameters. We show that obtaining optimal protocols past the slow-driving or linear response regime is computationally tractable as the sum of a friction tensor geodesic and a counterdiabatic term related to the Fisher information metric. These geodesic-counterdiabatic optimal protocols are exact for parametric harmonic potentials, reproduce the surprising nonmonotonic behavior recently discovered in linearly biased double well optimal protocols, and explain the ubiquitous discontinuous jumps observed at the beginning and end times.
Shortest-Path Percolation on Random Networks
We propose a bond-percolation model intended to describe the consumption, and eventual exhaustion, of resources in transport networks. Edges forming minimum-length paths connecting demanded origin-destination nodes are removed if below a certain budget. As pairs of nodes are demanded and edges are removed, the macroscopic connected component of the graph disappears, i.e., the graph undergoes a percolation transition. Here, we study such a shortest-path-percolation transition in homogeneous random graphs where pairs of demanded origin-destination nodes are randomly generated, and fully characterize it by means of finite-size scaling analysis. If budget is finite, the transition is identical to the one of ordinary percolation, where a single giant cluster shrinks as edges are removed from the graph; for infinite budget, the transition becomes more abrupt than the one of ordinary percolation, being characterized by the sudden fragmentation of the giant connected component into a multitude of clusters of similar size.
Had to read this again: self-organization vs growth, a great battle.
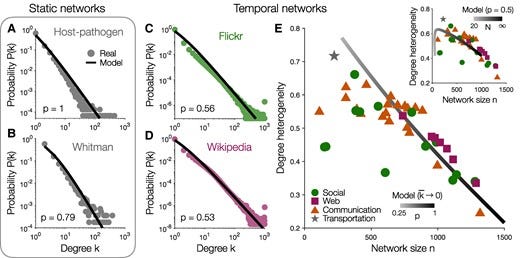
Many complex systems—from the Internet to social, biological, and communication networks—are thought to exhibit scale-free structure. However, prevailing explanations require that networks grow over time, an assumption that fails in some real-world settings. Here, we explain how scale-free structure can emerge without growth through network self-organization. Beginning with an arbitrary network, we allow connections to detach from random nodes and then reconnect under a mixture of preferential and random attachment. While the numbers of nodes and edges remain fixed, the degree distribution evolves toward a power-law with an exponent γ=1+1/p that depends only on the proportion p of preferential (rather than random) attachment. Applying our model to several real networks, we infer p directly from data and predict the relationship between network size and degree heterogeneity. Together, these results establish how scale-free structure can arise in networks of constant size and density, with broad implications for the structure and function of complex systems.
Mesoscale molecular assembly is favored by the active, crowded cytoplasm
The mesoscale organization of molecules into membraneless biomolecular condensates is emerging as a key mechanism of rapid spatiotemporal control in cells. Principles of biomolecular condensation have been revealed through in vitro reconstitution. However, intracellular environments are much more complex than test-tube environments: they are viscoelastic, highly crowded at the mesoscale, and are far from thermodynamic equilibrium due to the constant action of energy-consuming processes. We developed synDrops, a synthetic phase separation system, to study how the cellular environment affects condensate formation. Three key features enable physical analysis: synDrops are inducible, bioorthogonal, and have well-defined geometry. This design allows kinetic analysis of synDrop assembly and facilitates computational simulation of the process. We compared experiments and simulations to determine that macromolecular crowding promotes condensate nucleation but inhibits droplet growth through coalescence. ATP-dependent cellular activities help overcome the frustration of growth. In particular, stirring of the cytoplasm by actomyosin dynamics is the dominant mechanism that potentiates droplet growth in the mammalian cytoplasm by reducing confinement and elasticity. Our results demonstrate that mesoscale molecular assembly is favored by the combined effects of crowding and active matter in the cytoplasm. These results move toward a better predictive understanding of condensate formation in vivo.
Antifragility in complex dynamical systems
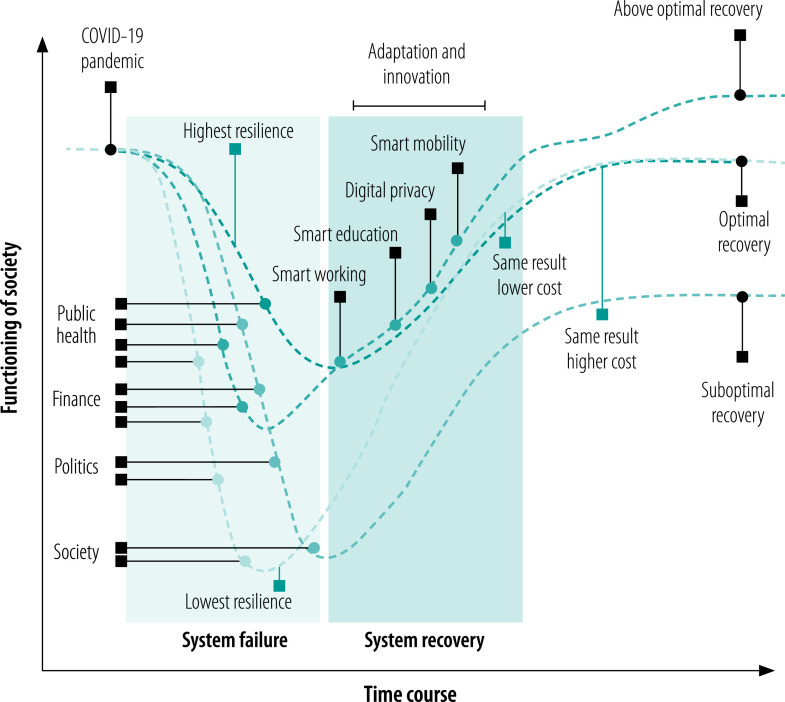
Surely it’s timely, since I was not following too much the literature about anti-fragility. However, I still struggle to understand what makes anti-fragility different from adaptiveness. The paper helps, but we need more mathematical definitions to differentiate between robustness, resilience, etc.
In a paper and in a previous post:
we have discussed about resilience and robustness in operational terms. I guess that anti-fragility should correspond to what we called “above-optimal recovery”?
[Yes, I agree, there is nothing above an optimum, or it would not be an optimum :)]
Besides the wording limitations, it is related to an adaptive response where the output state is “better” (according to some observer’s definition) than the input one.
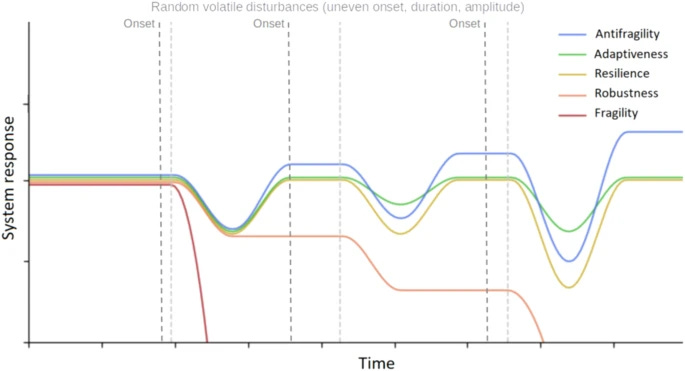
Antifragility characterizes the benefit of a dynamical system derived from the variability in environmental perturbations. Antifragility carries a precise definition that quantifies a system’s output response to input variability. Systems may respond poorly to perturbations (fragile) or benefit from perturbations (antifragile). In this manuscript, we review a range of applications of antifragility theory in technical systems (e.g., traffic control, robotics) and natural systems (e.g., cancer therapy, antibiotics). While there is a broad overlap in methods used to quantify and apply antifragility across disciplines, there is a need for precisely defining the scales at which antifragility operates. Thus, we provide a brief general introduction to the properties of antifragility in applied systems and review relevant literature for both natural and technical systems’ antifragility. We frame this review within three scales common to technical systems: intrinsic (input–output nonlinearity), inherited (extrinsic environmental signals), and induced (feedback control), with associated counterparts in biological systems: ecological (homogeneous systems), evolutionary (heterogeneous systems), and interventional (control). We use the common noun in designing systems that exhibit antifragile behavior across scales and guide the reader along the spectrum of fragility–adaptiveness–resilience–robustness–antifragility, the principles behind it, and its practical implications.
Biological Systems
How Does a Molecule Become a Message?
This paper is a good reading before the next one, from Pattee too:
The theme of this symposium is “Communication in Development,” and, as an outsider to the field of developmental biology, I am going to begin by asking a question: How do we tell when there is communication in living systems? Most workers in the field probably do not worry too much about defining the idea of communication since so many concrete, experimental questions about developmental control do not depend on what communication means. But I am interested in the origin of life, and I am convinced that the problem of the origin of life cannot even be formulated without a better understanding of how molecules can function symbolically, that is, as records, codes, and signals. Or as I imply in my title, to understand origins, we need to know how a molecule becomes a message.
Symbol Grounding Precedes Interpretation
There is an interesting take at the end of this paper:
I concluded then, and I still believe, that speculative models and computer simulations can never solve the origin problem. […] More experiments are needed simulating realistically complex sterile earth environments, like sterile seashores with sand, clays, tides, surf and diurnal radiation, hydrothermal vents, etc
Deacon speculates on the origin of interpretation of signs using autocatalytic origin of life models and Peircean terminology. I explain why interpretation evolved only later as a triadic intervention between symbols and actions. In all organisms the passive one-dimensional genetic informational symbol sequences are converted to active functional proteins or nucleic acids by three-dimensional folding. This symbol grounding is a direct symbol-to-action conversion. It is universal throughout all evolution. Folding is entirely a lawful physical process, leaving neither freedom nor necessity for interpretation. Similarly, the initial converse action-to-symbol conversion of sensory inputs also leaves no freedom for interpretation until after the action-to-symbol conversion.
Fungal mycelium networks are large scale biological networks along which nutrients, metabolites flow. Recently, we discovered a rich spectrum of electrical activity in mycelium networks, including action-potential spikes and trains of spikes. Reasoning by analogy with animals and plants, where travelling patterns of electrical activity perform integrative and communicative mechanisms, we speculated that waves of electrical activity transfer information in mycelium networks. Using a new discrete space–time model with emergent radial spanning-tree topology, hypothetically comparable mycelial morphology and physically comparable information transfer, we provide physical arguments for the use of such a model, and by considering growing mycelium network by analogy with growing network of matter in the cosmic web, we develop mathematical models and theoretical concepts to characterise the parameters of the information transfer.
Neuroscience
The UK Biobank data is a gold mine.
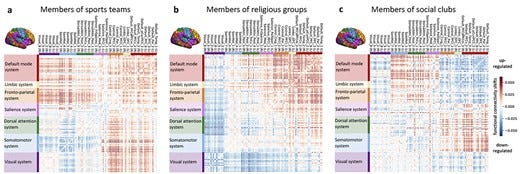
Human behavior across the life span is driven by the psychological need to belong, right from kindergarten to bingo nights. Being part of social groups constitutes a backbone for communal life and confers many benefits for the physical and mental health. Capitalizing on the neuroimaging and behavioral data from ∼40,000 participants from the UK Biobank population cohort, we used structural and functional analyses to explore how social participation is reflected in the human brain. Across 3 different types of social groups, structural analyses point toward the variance in ventromedial prefrontal cortex, fusiform gyrus, and anterior cingulate cortex as structural substrates tightly linked to social participation. Functional connectivity analyses not only emphasized the importance of default mode and limbic network but also showed differences for sports teams and religious groups as compared to social clubs. Taken together, our findings establish the structural and functional integrity of the default mode network as a neural signature of social belonging.
Power and reproducibility in the external validation of brain-phenotype predictions
Brain-phenotype predictive models seek to identify reproducible and generalizable brain-phenotype associations. External validation, or the evaluation of a model in external datasets, is the gold standard in evaluating the generalizability of models in neuroimaging. Unlike typical studies, external validation involves two sample sizes: the training and the external sample sizes. Thus, traditional power calculations may not be appropriate. Here we ran over 900 million resampling-based simulations in functional and structural connectivity data to investigate the relationship between training sample size, external sample size, phenotype effect size, theoretical power and simulated power. Our analysis included a wide range of datasets: the Healthy Brain Network, the Adolescent Brain Cognitive Development Study, the Human Connectome Project (Development and Young Adult), the Philadelphia Neurodevelopmental Cohort, the Queensland Twin Adolescent Brain Project, and the Chinese Human Connectome Project; and phenotypes: age, body mass index, matrix reasoning, working memory, attention problems, anxiety/depression symptoms and relational processing. High effect size predictions achieved adequate power with training and external sample sizes of a few hundred individuals, whereas low and medium effect size predictions required hundreds to thousands of training and external samples. In addition, most previous external validation studies used sample sizes prone to low power, and theoretical power curves should be adjusted for the training sample size. Furthermore, model performance in internal validation often informed subsequent external validation performance (Pearson’s r difference <0.2), particularly for well-harmonized datasets. These results could help decide how to power future external validation studies.
Eating and Cognition in Two Animals without Neurons: Sponges and Trichoplax
There is nothing better than two systems without neurons to discuss in the neuroscience section of the newsletter… but this is great to trigger future discussions with my neuro-friends.
There are also animals that lack neurons but process information in order to maintain themselves
Eating is a fundamental behavior in which all organisms must engage in order to procure the material and energy from their environment that they need to maintain themselves. Since controlling eating requires procuring, processing, and assessing information, it constitutes a cognitive activity that provides a productive domain for pursuing cognitive biology as proposed by Ladislav Kováč. In agreement with Kováč, we argue that cognition is fundamentally grounded in chemical signaling and processing. To support this thesis, we adopt Cisek’s strategy of phylogenetic refinement, focusing on two animal phyla, Porifera and Placozoa, organisms that do not have neurons, muscles, or an alimentary canal, but nonetheless need to coordinate the activity of cells of multiple types in order to eat. We review what research has revealed so far about how these animals gather and process information to control their eating behavior.
Centering cognitive neuroscience on task demands and generalization
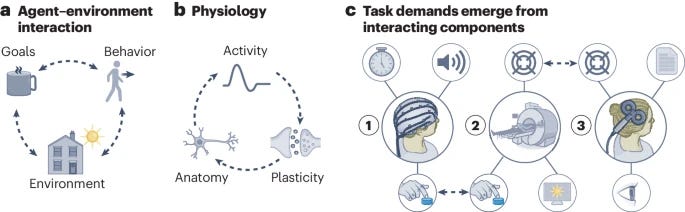
Cognitive neuroscience seeks generalizable theories explaining the relationship between behavioral, physiological and mental states. In pursuit of such theories, we propose a theoretical and empirical framework that centers on understanding task demands and the mutual constraints they impose on behavior and neural activity. Task demands emerge from the interaction between an agent’s sensory impressions, goals and behavior, which jointly shape the activity and structure of the nervous system on multiple spatiotemporal scales. Understanding this interaction requires multitask studies that vary more than one experimental component (for example, stimuli and instructions) combined with dense behavioral and neural sampling and explicit testing for generalization across tasks and data modalities. By centering task demands rather than mental processes that tasks are assumed to engage, this framework paves the way for the discovery of new generalizable concepts unconstrained by existing taxonomies, and moves cognitive neuroscience toward an action-oriented, dynamic and integrated view of the brain.
(Human) behavior
Complex behavior from intrinsic motivation to occupy future action-state path space
Initially I was really wondering about the differences with an older paper on causal entropic forces, but then I discovered that the manuscript makes a fair job in positioning in the literature and it is very interesting how some complex behaviors can emerge in absence of reward-maximizing principles.
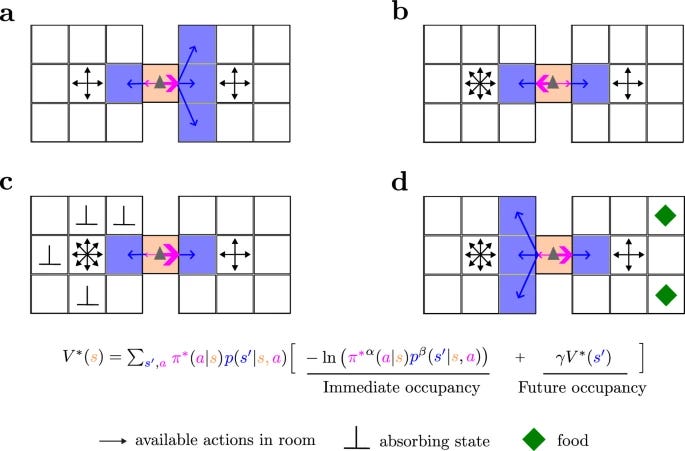
Although MOP agents do not have any extrinsically designed goal, like eating or escaping, they generate these deterministic, goal-directed behaviors whenever necessary so that they can keep moving in the future and maximize future path action-state entropy
Most theories of behavior posit that agents tend to maximize some form of reward or utility. However, animals very often move with curiosity and seem to be motivated in a reward-free manner. Here we abandon the idea of reward maximization and propose that the goal of behavior is maximizing occupancy of future paths of actions and states. According to this maximum occupancy principle, rewards are the means to occupy path space, not the goal per se; goal-directedness simply emerges as rational ways of searching for resources so that movement, understood amply, never ends. We find that action-state path entropy is the only measure consistent with additivity and other intuitive properties of expected future action-state path occupancy. We provide analytical expressions that relate the optimal policy and state-value function and prove convergence of our value iteration algorithm. Using discrete and continuous state tasks, including a high-dimensional controller, we show that complex behaviors such as “dancing”, hide-and-seek, and a basic form of altruistic behavior naturally result from the intrinsic motivation to occupy path space. All in all, we present a theory of behavior that generates both variability and goal-directedness in the absence of reward maximization.