Complexity Thoughts: Issue #68
Unraveling complexity: building knowledge, one paper at a time
If you find value in #ComplexityThoughts, consider helping it grow by subscribing and sharing it with friends, colleagues or on social media. Your support makes a real difference.
→ Don’t miss the podcast version of this post: click on “Spotify/Apple Podcast” above!
Foundations of network science and complex systems
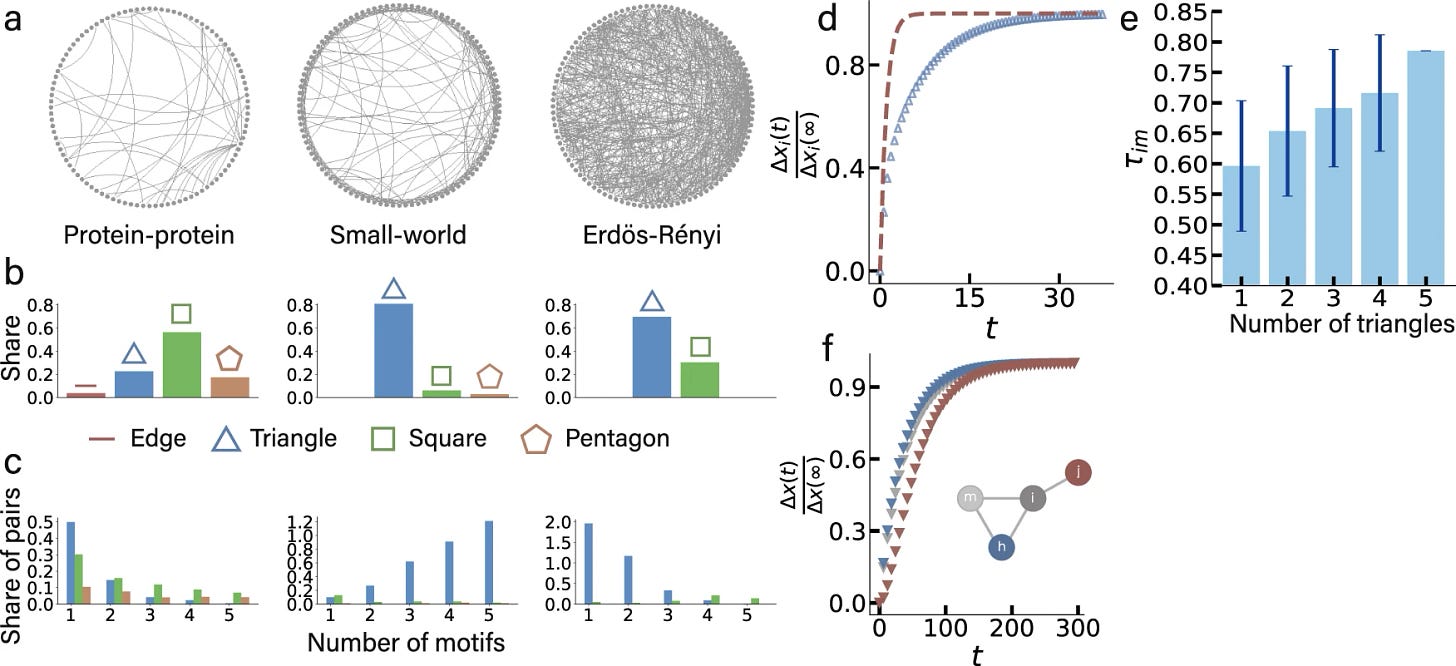
Impact of basic network motifs on the collective response to perturbations
Many collective phenomena such as epidemic spreading and cascading failures in socioeconomic systems on networks are caused by perturbations of the dynamics. How perturbations propagate through networks, impact and disrupt their functions may depend on the network, the type and location of the perturbation as well as the spreading dynamics. Previous work has analyzed the retardation effects of the nodes along the propagation paths, suggesting a few transient propagation "scaling” regimes as a function of the nodes’ degree, but regardless of motifs such as triangles. Yet, empirical networks consist of motifs enabling the proper functioning of the system. Here, we show that basic motifs along the propagation path jointly determine the previously proposed scaling regimes of distance-limited propagation and degree-limited propagation, or even cease their existence. Our results suggest a radical departure from these scaling regimes and provide a deeper understanding of the interplay of self-dynamics, interaction dynamics, and topological properties.
On the roles of function and selection in evolving systems
I am reading again this paper, after a while. And still, I think that it is a very pleasant article to read, while I miss the quantitative aspects to make this theory fully falsifiable. What do you think?
Is this “law of increasing functional information” really a law, or is more like a conjecture? By the way, I agree with the rationale.
The universe is replete with complex evolving systems, but the existing macroscopic physical laws do not seem to adequately describe these systems. Recognizing that the identification of conceptual equivalencies among disparate phenomena were foundational to developing previous laws of nature, we approach a potential “missing law” by looking for equivalencies among evolving systems. We suggest that all evolving systems—including but not limited to life—are composed of diverse components that can combine into configurational states that are then selected for or against based on function. We then identify the fundamental sources of selection—static persistence, dynamic persistence, and novelty generation—and propose a time-asymmetric law that states that the functional information of a system will increase over time when subjected to selection for function(s).
Systems of many interacting agents display an increase in diversity, distribution, and/or patterned behavior when numerous configurations of the system are subject to selective pressure.
Physical laws—such as the laws of motion, gravity, electromagnetism, and thermodynamics—codify the general behavior of varied macroscopic natural systems across space and time. We propose that an additional, hitherto-unarticulated law is required to characterize familiar macroscopic phenomena of our complex, evolving universe. An important feature of the classical laws of physics is the conceptual equivalence of specific characteristics shared by an extensive, seemingly diverse body of natural phenomena. Identifying potential equivalencies among disparate phenomena—for example, falling apples and orbiting moons or hot objects and compressed springs—has been instrumental in advancing the scientific understanding of our world through the articulation of laws of nature. A pervasive wonder of the natural world is the evolution of varied systems, including stars, minerals, atmospheres, and life. These evolving systems appear to be conceptually equivalent in that they display three notable attributes: 1) They form from numerous components that have the potential to adopt combinatorially vast numbers of different configurations; 2) processes exist that generate numerous different configurations; and 3) configurations are preferentially selected based on function. We identify universal concepts of selection—static persistence, dynamic persistence, and novelty generation—that underpin function and drive systems to evolve through the exchange of information between the environment and the system. Accordingly, we propose a “law of increasing functional information”: The functional information of a system will increase (i.e., the system will evolve) if many different configurations of the system undergo selection for one or more functions.
Theory of first-order phase transitions
This paper by Binder is getting old (almost 40 years), but it’s a great one if you want to deal with first-order phase transitions.
An introductory review of various concepts about first-order phase transitions is given. Rules for classification of phase transitions as second or first order are discussed, as well as exceptions to these rules. Attention is drawn to the rounding of first-order transitions due to finite-size or quenched impurities. Computational methods to calculate phase diagrams for simple model Hamiltonians are also described. Particular emphasis is laid on metastable states near first-order phase transitions, on the 'stability limits' of such states (e.g. the 'spinodal curve' of the gas-liquid transition) and on the dynamic mechanisms by which metastable states decay (nucleation and growth of droplets of a new phase, etc.).
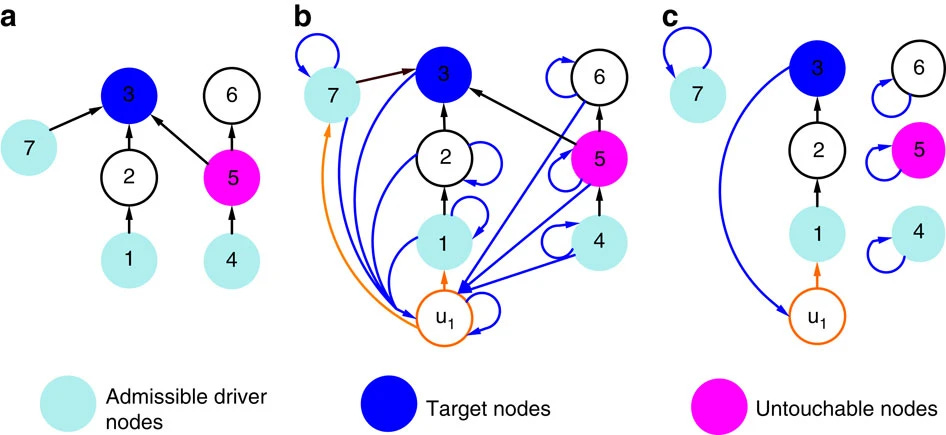
Structural permeability of complex networks to control signals
Many biological, social and technological systems can be described as complex networks. The goal of affecting their behaviour has motivated recent work focusing on the relationship between the network structure and its propensity to be controlled. While this work has provided insight into several relevant problems, a comprehensive approach to address partial and complete controllability of networks is still lacking. Here, we bridge this gap by developing a framework to maximize the diffusion of the control signals through a network, while taking into account physical and economic constraints that inevitably arise in applications. This approach allows us to introduce the network permeability, a unified metric of the propensity of a network to be controllable. The analysis of the permeability of several synthetic and real networks enables us to extract some structural features that deepen our quantitative understanding of the ease with which specific controllability requirements can be met.
Colloquium: Eigenvector continuation and projection-based emulators
Eigenvector continuation is a computational technique designed to solve very large eigenvalue problems — like the ones we have in quantum many-body physics and, why not, complex systems — by reducing them to a much smaller, more manageable form. The key idea is that the eigenvectors of a Hamiltonian (or similar operator) change smoothly when you vary a control parameter, such as the strength of an interaction. Because of this smoothness, the family of eigenvectors you would encounter as the parameter varies actually lies close to a low-dimensional subspace.
The method exploits this by taking a handful of “snapshots” of exact eigenvectors at selected parameter values and then constructing a reduced variational subspace from them. Once built, this subspace can be used to efficiently approximate eigenvalues and eigenvectors at new parameter values, without having to solve the original, enormous problem again. It is cool because often converges much faster than standard perturbation theory, especially in challenging regimes where traditional expansions might break down.
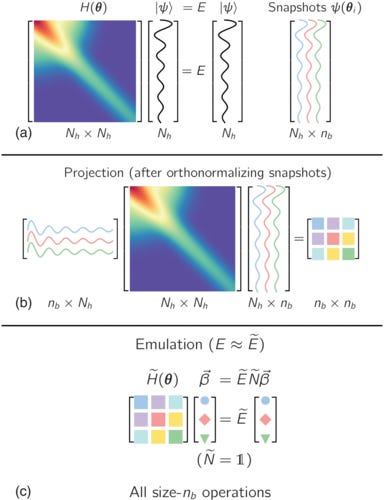
Eigenvector continuation is a computational method for parametric eigenvalue problems that uses subspace projection with a basis derived from eigenvector snapshots from different parameter sets. It is part of a broader class of subspace-projection techniques called reduced-basis methods. In this Colloquium, the development, theory, and applications of eigenvector continuation and projection-based emulators are presented. The basic concepts are introduced, the underlying theory and convergence properties are discussed, and recent applications for quantum systems and future prospects are presented.
Self-Organized and Driven Phase Synchronization in Coupled Maps
We study the phase synchronization and cluster formation in coupled maps on different networks. We identify two different mechanisms of cluster formation: (a) self-organized phase synchronization which leads to clusters with dominant intracluster couplings and (b) driven phase synchronization which leads to clusters with dominant intercluster couplings. In the novel driven synchronization the nodes of one cluster are driven by those of the others. We also discuss the dynamical origin of these two mechanisms for small networks with two and three nodes.
Complexity and synchronization
We study a fully connected network (cluster) of interacting two-state units as a model of cooperative decision making. Each unit in isolation generates a Poisson process with rate 𝑔. We show that when the number of nodes is finite, the decision-making process becomes intermittent. The decision-time distribution density is characterized by inverse power-law behavior with index 𝜇=1.5 and is exponentially truncated. We find that the condition of perfect consensus is recovered by means of a fat tail that becomes more and more extended with increasing number of nodes 𝑁. The intermittent dynamics of the global variable are described by the motion of a particle in a double well potential. The particle spends a portion of the total time 𝜏𝑆 at the top of the potential barrier. Using theoretical and numerical arguments it is proved that 𝜏𝑆∝(1/𝑔)ln(const×𝑁). The second portion of its time, 𝜏𝐾, is spent by the particle at the bottom of the potential well and it is given by 𝜏𝐾=(1/𝑔)exp(const×𝑁). We show that the time 𝜏𝐾 is responsible for the Kramers fat tail. This generates a stronger ergodicity breakdown than that generated by the inverse power law without truncation. We establish that the condition of partial consensus can be transmitted from one cluster to another provided that both networks are in a cooperative condition. No significant information transmission is possible if one of the two networks is not yet self-organized. We find that partitioning a large network into a set of smaller interacting clusters has the effect of converting the fat Kramers tail into an inverse power law with 𝜇=1.5.
Chaotic but regular posi-nega switch among coded attractors by cluster-size variation
A globally coupled map lattice is investigated. A simple coding of many attractors with clustering is shown. Through the coding, the attractors are organized so that their change exhibits the period-doubling bifurcation. By a simple input on a site, we can switch among attractors and tune the strength of chaos. A threshold on the cluster size is found beyond which a peculiar ‘‘posi-nega’’ switch occurs.
Biological Systems
Metabolites are not genes — avoiding the misuse of pathway analysis in metabolomics
The misuse of analytical methods is a problem affecting every discipline.
Pathway analysis, originally developed for gene expression data, has been adapted for metabolomics. However, owing to the unique characteristics and constraints of metabolites compared with genes, pathway analysis in metabolomics often yields misleading or nonsensical results.
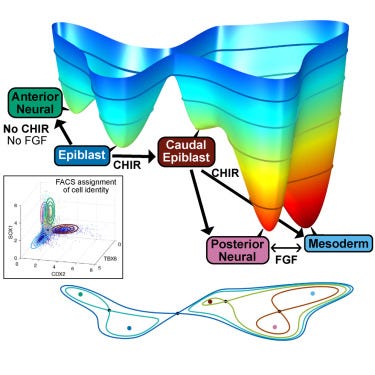
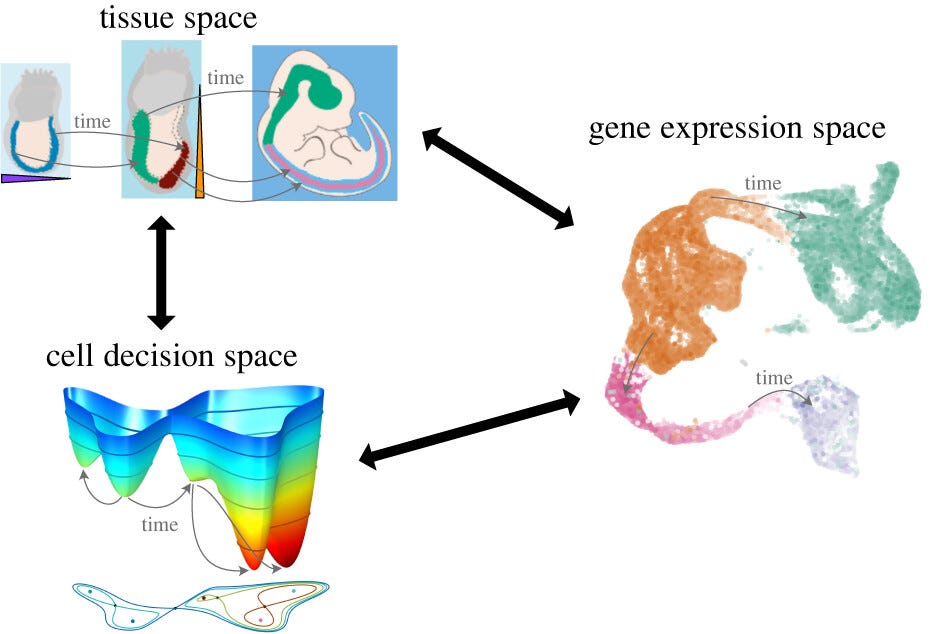
Dynamical landscapes of cell fate decisions
Waddington offered one of the most enduring metaphors in developmental biology: he imagined a cell as a marble rolling down a branching landscape of valleys, each split representing a choice of fate. Would it become a nerve cell, a muscle cell or something else entirely? For decades this image remained more poetic than predictive, a way to think rather than to calculate. In this paper, which is a review (a very good one, indeed), the authors make an effort to put mathematics beneath the metaphor.
By drawing on catastrophe theory — a framework designed to capture sudden shifts — and the powerful language of dynamical systems, the Waddington’s sketch is “translated” into quantitative models. Remarkably, this work suggests that despite the staggering variety of cell types, the fundamental “decision-making” machinery of cells comes down to just two possible modes when faced with a binary choice. This is not only a deep simplification of an apparently intractable process but also a tool: models of this kind can be calibrated with experimental data to predict how cells will behave. It’s a great example of how even the most complex aspects of life may follow a surprisingly small set of rules, hidden in the geometry of change.
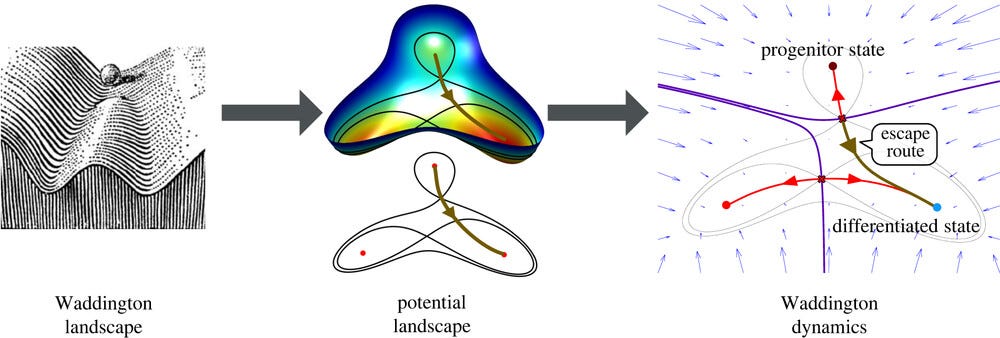
The generation of cellular diversity during development involves differentiating cells transitioning between discrete cell states. In the 1940s, the developmental biologist Conrad Waddington introduced a landscape metaphor to describe this process. The developmental path of a cell was pictured as a ball rolling through a terrain of branching valleys with cell fate decisions represented by the branch points at which the ball decides between one of two available valleys. Here we discuss progress in constructing quantitative dynamical models inspired by this view of cellular differentiation. We describe a framework based on catastrophe theory and dynamical systems methods that provides the foundations for quantitative geometric models of cellular differentiation. These models can be fit to experimental data and used to make quantitative predictions about cellular differentiation. The theory indicates that cell fate decisions can be described by a small number of decision structures, such that there are only two distinct ways in which cells make a binary choice between one of two fates. We discuss the biological relevance of these mechanisms and suggest the approach is broadly applicable for the quantitative analysis of differentiation dynamics and for determining principles of developmental decisions.
Fate decisions in developing tissues involve cells transitioning between discrete cell states, each defined by distinct gene expression profiles. The Waddington landscape, in which the development of a cell is viewed as a ball rolling through a valley filled terrain, is an appealing way to describe differentiation. To construct and validate accurate landscapes, quantitative methods based on experimental data are necessary. We combined principled statistical methods with a framework based on catastrophe theory and approximate Bayesian computation to formulate a quantitative dynamical landscape that accurately predicts cell fate outcomes of pluripotent stem cells exposed to different combinations of signaling factors. Analysis of the landscape revealed two distinct ways in which cells make a binary choice between one of two fates. We suggest that these represent archetypal designs for developmental decisions. The approach is broadly applicable for the quantitative analysis of differentiation and for determining the logic of developmental decisions.
the view that genes are the primary causal agents of all the phenomena of organismic life is not well supported by the findings of contemporary biology — Nicholson (2010)
Jacques Monod famously said that ‘What is true for E. coli is true for the elephant.’ While this might be correct in the basic sense that both use nucleic acids and proteins, it is no longer clear that they use them in quite the same way. The many qualitative differences in the biomolecular constitution and mechanisms of protozoans and metazoans, from the proportions of non-coding DNA to those of multidomain and disordered proteins and the mechanisms of gene regulation, seem to reflect different generic principles in how the two types of organism operate at the molecular and cellular levels. Here I suggest that one way to think about those differences is as a shift in the locus of biological causation – a shift that has implications for making biomedical interventions in humans.
→ Please, remind that if you find value in #ComplexityThoughts, you might consider helping it grow by subscribing, or by sharing it with friends, colleagues or on social media. See also this post to learn more about this space.