Following up on Assembly Theory
More from the ongoing academic debate
Dall-e 3 representation of this issue’s content
In a previous post I have tried to make a summary of a recent paper about Assembly Theory, also through the voice of some colleagues in the community. Many words were spent in social media and personal blogs, at that time.
Recently, two new papers appeared, building on those arguments to move the discussion to a more academic level:
Assembly Theory: What It Does and What It Does Not Do
A recent publication in Nature has generated much heated discussion about evolution, its tendency towards increasing diversity and complexity, and its potential status above and beyond the known laws of fundamental physics. The argument at the heart of this controversy concerns assembly theory, a method to detect and quantify the influence of higher-level emergent causal constraints in computational worlds made of basic objects and their combinations. In this short essay, I briefly review the theory, its basic principles and potential applications. I then go on to critically examine its authors’ assertions, concluding that assembly theory has merit but is not nearly as novel or revolutionary as claimed. It certainly does not provide any new explanation of biological evolution or natural selection, or a new grounding of biology in physics. In this regard, the presentation of the paper is starkly distorted by hype, which may explain some of the outrage it created.
Here, Jaeger explicitly writes that he “finds assembly theory intriguing and worth considering”, elucidating why the theory is interesting. In parallel, he identifies the main issues with the way the theory has been presented and published.
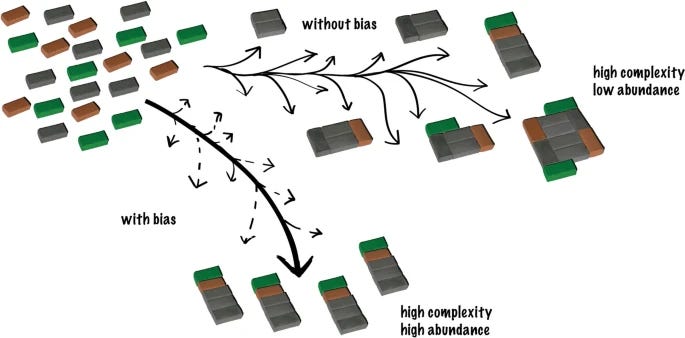
What assembly theory really does is to detect and quantify bias caused by higher-level constraints in some well-defined rule-based worlds. That’s it! Even if Darwinian selection may contribute to such bias, assembly theory cannot tell you if it does, how much it does, or if other factors play a role as well. — Johannes Jaeger
In the other paper, the authors show how Assembly Theory, in its current formulation, can be understood in terms of algorithmic complexity.
We demonstrate that Assembly Theory, pathway complexity, the assembly index, and the assembly number are subsumed and constitute a weak version of algorithmic (Kolmogorov-Solomonoff-Chaitin) complexity reliant on an approximation method based upon statistical compression, their results obtained due to the use of methods strictly equivalent to the LZ family of compression algorithms used in compressing algorithms such as ZIP, GZIP, or JPEG. Such popular algorithms have been shown to empirically reproduce the results of AT's assembly index and their use had already been reported in successful application to separating organic from non-organic molecules, and the study of selection and evolution. Here we exhibit and prove the connections and full equivalence of Assembly Theory to Shannon Entropy and statistical compression, and AT's disconnection as a statistical approach from causality. We demonstrate that formulating a traditional statistically compressed description of molecules, or the theory underlying it, does not imply an explanation or quantification of biases in generative (physical or biological) processes, including those brought about by selection and evolution, when lacking in logical consistency and empirical evidence. We argue that in their basic arguments, the authors of AT conflate how objects may assemble with causal directionality, and conclude that Assembly Theory does nothing to explain selection or evolution beyond known and previously established connections, some of which are reviewed here, based on sounder theory and better experimental evidence.
The main concerns follow a systematic set of arguments, also reflected in the structure of the paper:
The assembly Index is a compression algorithm of the LZ family
A compression algorithm is a mechanical procedure that corresponds to a physical process
Conflating object assembly process and causation directionality
Lack of control experiments and absence of supporting empirical data beyond current domain knowledge
The authors show that, from a technical perspective, “assembly theory is an approximation to algorithmic complexity” and the “assembly index defines a grammar of compression that is bounded by LZ compression and can at most approximate the Shannon Entropy rate”.
The suggestions made by Assembly Theory that people may resonate with, only highlight the working hypothesis that information theory, algorithmic complexity, and algorithmic probability underpin the processes and building blocks of physical and living systems on which all these methods and frameworks have been heavily inspired upon [48, 49], playing an important role in chemical processes [17], nature and biology as suggested before. — Abrahão et al
The debate is ongoing, and it will be interesting to see its evolution through the traditional academic channels, rather than social media and press releases.
I think that this discussion will only enrich the academic community as a whole, highlighting the credits, and the debts, of Assembly Theory in the broader framework of information theory and complexity science.