Making sense of complex systems functionality
What slime molds, neural systems and quantum physics have in common?
If you find value in #ComplexityThoughts, consider helping it grow by subscribing and sharing it with friends, colleagues or on social media. Your support makes a real difference.
→ Don’t miss the podcast version of this post: click on “Spotify/Apple Podcast” above!
Introduction
How can a tiny organism survive boiling heat, crushing pressure or even the vacuum of the outer space, while our most advanced infrastructures collapse under a summer storm?
In this post I provide an overview that is inspired by my recent keynote in Siena at the Conference on Complex Systems.
Structurally, complex systems are more than the sum of their connections. But functionally, their survival hinges on what these networks allow them to do: process information, cooperate, regenerate, optimize under constraints, so forth and so on. From cells to societies, functionality is the hidden layer that determines resilience and adaptation. Yet most of network science has focused on structure — ie., on who connects to whom — rather than on function: how systems decide, remember or recover.

Consider the tardigrade. For nearly half a billion years, this microscopic animal has endured extremes, temperatures close to absolute zero, radiation thousands of times higher than lethal human doses and the vacuum of outer space. Its robustness is not encoded in a single molecule, but in a distributed network of protective mechanisms that work together.
Video: A leaky integrate and fire model running on the top of the fruit fly connectome. Source: Shiu et al.
The same riddle appears in gene regulatory networks, protein–protein interactions, metabolic and neural circuits, and even in the power grids that keep our cities alive: survival depends not just on connections, but on the functional rules those connections enable.
Some great illustrations come from the living world, and I have discussed them during my talk. Slime molds (Dictyostelium polycephalum) are single-celled organisms with no central control that can collectively solve mazes and optimize nutrient pathways, effectively computing efficient networks of transport without neurons or brains. Their functionality emerges from local rules of aggregation and chemical signaling, scaled up into a form of collective intelligence.
Similarly, fire ants exhibit striking resilience under stress. When floods threaten their colonies, thousands of individuals interlock their bodies to form buoyant rafts. These living platforms not only keep the colony afloat but also reorganize dynamically, redistributing weight and maintaining cohesion until safe ground is found. What looks like instinct is in fact distributed problem-solving: functionality arising from cooperation and physical coupling.
These principles scale far beyond biology. Take the climate system, coral reefs and industrial infrastructures, which are tightly interdependent: ice sheets regulate ocean circulation; coral reefs buffer coastlines and sustain biodiversity; human activities inject greenhouse gases that destabilize both. Functionality here is not a property of one subsystem, but of the coupled whole: weakening one link triggers cascading failures that propagate across climate, ecology and society. The same feedback loops that ensure resilience can, under pressure, amplify fragility: reminding us that interdependence is both the source of robustness and the pathway to collapse.
The 2021 blackout in New Orleans is a stark reminder that structure alone does not guarantee function. The power grid and urban infrastructure remained physically in place after Hurricane Ida, yet electricity, mobility and communication collapsed. The network’s skeleton survived, but its functionality — coordinating flows of energy and information — was fatally disrupted. This illustrates the critical distinction: a system can look intact structurally while being effectively useless functionally.
I think that there is a predictive gap: without a unifying framework, we remain unable to anticipate when a system will withstand perturbation or collapse under stress. And I have no final solution to this problem (yet!).
Why we need a new framework
Plato warned that we might mistake shadows for reality.

In complexity science, our models risk the same: simplified projections of phenomena onto a narrow wall of observables. Traditional modeling encodes initial conditions, evolves them with hypothesized rules and compares predicted outcomes with reality. But the choice of observables, the formalism applied and the assumptions we make already filter the system through our own torchlight.
In complex systems, this reduction might just fail. Multiple constraints compete and dynamics unfold across high-dimensional, rugged landscapes where local optima abound. Observation is not reality: it is a biased cross-section. What matters is the phenomenon itself, independent of its substrate, whether biochemical, social or technological (as per Langton, 1989).
What are the implications? In a nutshell:
Model-dependence: our predictions depend less on “laws of nature” and more on how we encode observables.
Principles over details: variational approaches, from least action to maximum entropy, show that many features can be inferred by extremizing a suitable quantity under constraints.
Micro–macro gap: bridging local interactions with emergent functionality requires ensemble methods, operator algebra and entropy-based reasoning (to say the least).
To move beyond shadows, we must find (or build by scratch) a predictive framework where functionality emerges not from static wiring but from the algebra of interactions and the probabilistic ensembles of possible states unfolding on the top of an adaptive network.
Building the Density Matrix formalism
To bridge micro-level interactions with emergent functionality, we need a representation that preserves information while scaling across dimensions. Traditional network models capture who connects to whom; dynamical models add how states evolve. But to study functionality, we must treat events on networks — i.e., the propagation of perturbations, signals, or decisions — as the true carriers of information: static networks alone or static signal flows are not enough.
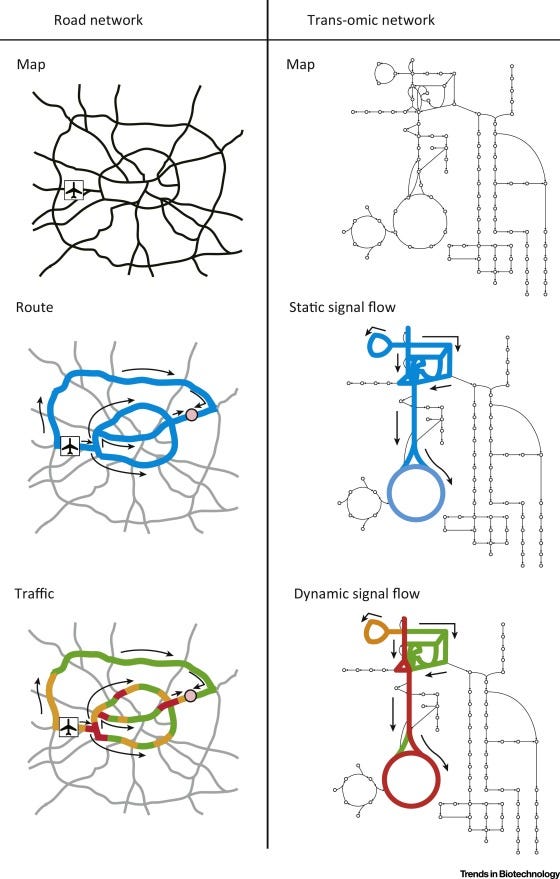
Static connectivity tells us only where signals could travel, not how they actually move. The same road map can host an empty street at midnight or a traffic jam at rush hour; the structure is identical, but the functionality is radically different. Biological and technological networks are no different: the pattern of interactions can channel information smoothly in one regime and block it entirely in another. This simple fact has several implications:
Identical structure, different dynamics: a neural circuit can sustain oscillations, diffusion, or avalanches depending on which process unfolds, yielding very different functional outcomes.
Identical dynamics, different parameters: an epidemic model above the threshold spreads globally; just below it, infections remain localized, even though the network is the same.
Functional outcomes diverge: as we have shown in a recent work, the latent geometry induced by dynamics often mismatches the topology: structural modules can either trap perturbations or become transparent, depending on the dynamical regime.
So, functionality cannot be read off the wiring diagram (unless specific conditions are met): it emerges.
Borrowing from thermodynamics and quantum mechanics, we can represent system states as vectors evolving under operators. Why? Well, to keep this post as readable as possible without too much technicalities, I refer to another post where this is explained with some flavor:
Here, I focus on explaining what we can do, operationally. Instead of tracking one trajectory, we must build a density matrix ρ(𝜏), which encodes the statistical ensemble of all possible perturbation pathways at a given integration scale 𝜏.
The starting point is to define a microstate, to allow us to count microstates to build a statistical physics. Below I show how the density matrix formalism captures functionality as ensembles of events, not just connections. Each perturbation defines a possible information pathway, and together these pathways reveal how a network processes signals across scales, preserving the dynamics that structure alone cannot explain.
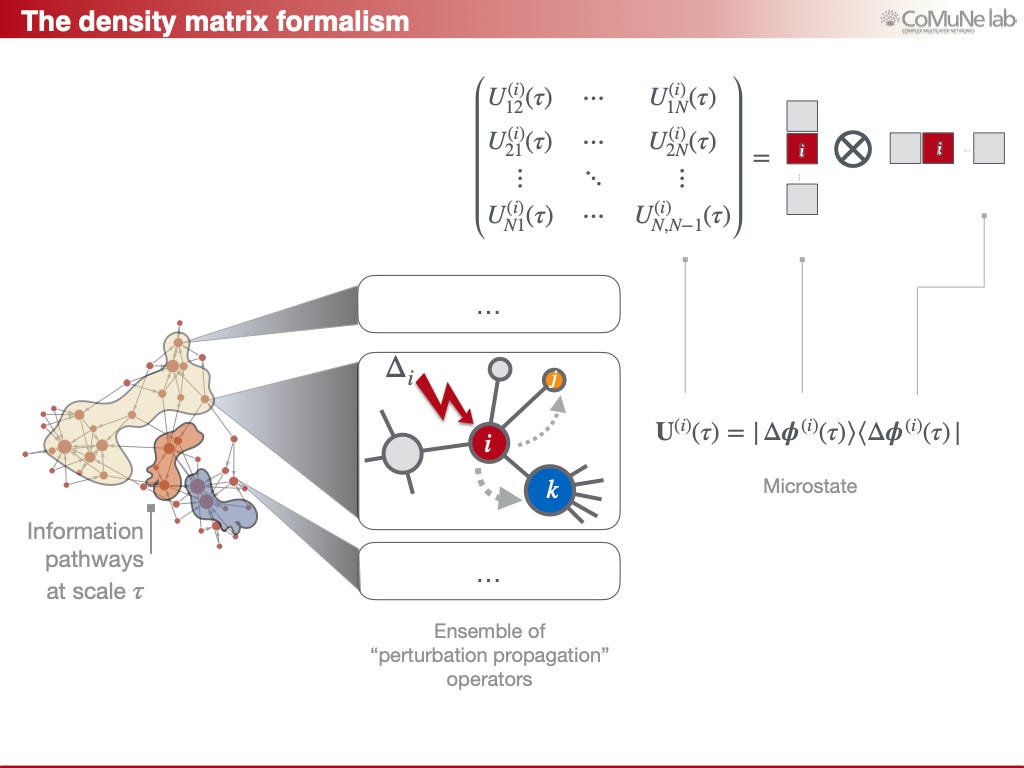
From here, we can define the density matrix as a statistical ensemble that accounts for the weighted contribution of each microstate:
This allows us to build on the definition of the entropy given by Von Neumann in for quantum systems:
Its interpretation is, however, somehow different from the quantum-mechanical one (i.e., measuring uncertainty about quantum states): here, our entropy quantifies the diversity of configurations accessible to the system in terms of activation in response to perturbations. Our entropy emphasizes functional flexibility rather than quantum uncertainty, making the analogy precise but not identical, of course.
But what if we have no good guesses about the underlying dynamics?
When the microscopic dynamics are unknown, the principle of maximum entropy provides closure: the least biased distribution consistent with observed constraints yields a simple form which looks like the propagator of a diffusion-like process.

This guarantees that our description of functionality is not an artifact of modeling assumptions, but an inference grounded in statistical consistency. Furthermore, we can appreciate how 𝜏 provides a natural lens to integrate dynamics across scales, from rapid signaling to long-term adaptation. Modularity and hierarchy keep entropy “alive” and persistent, thus enabling systems to sustain diverse responses and resist collapse.
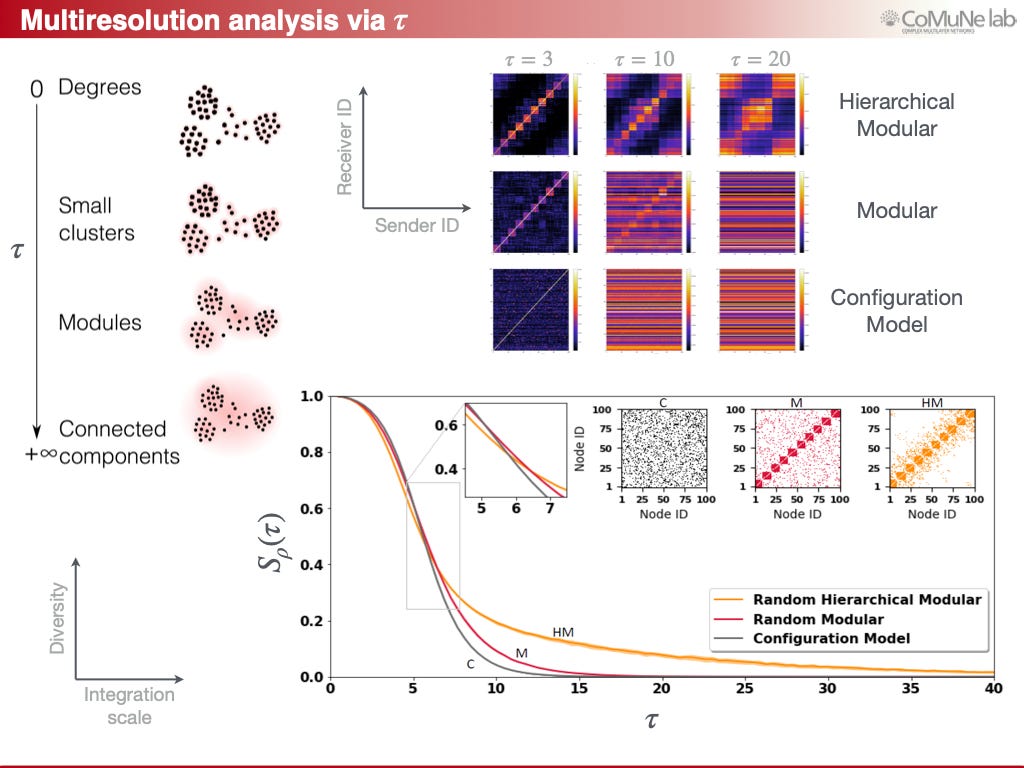
With this formalism, we can now quantify how functionality emerges, persists or erodes in practice, (almost) regardless if we consider genetic circuits, neural systems or infrastructures under stress.
Applications!
What good is a predictive framework if it cannot be tested? We stress-tested our approach against two fundamental problems: robustness and sparsity.
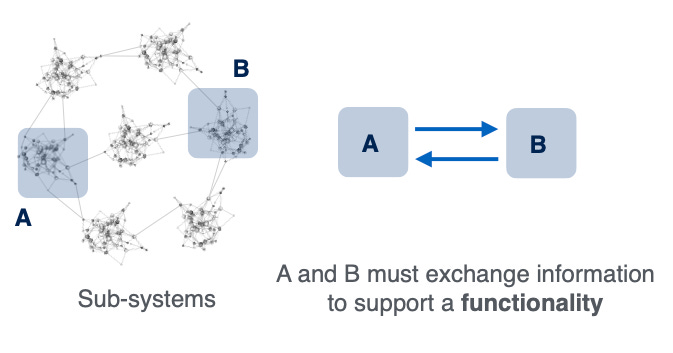
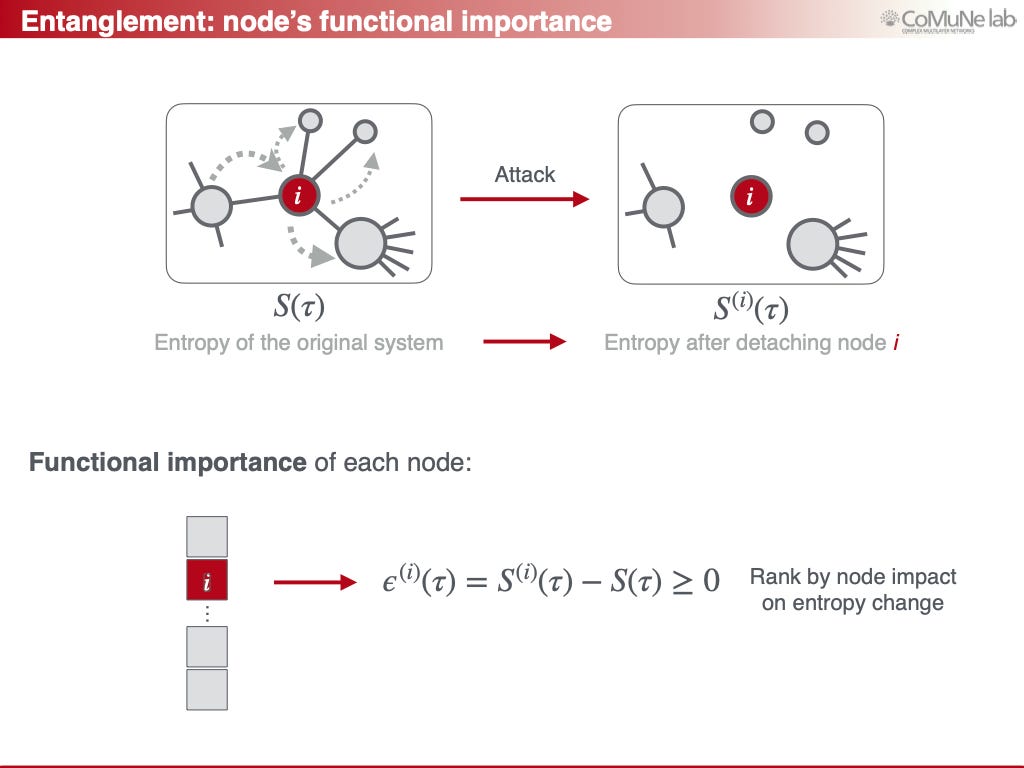
Functional Robustness. Traditional resilience studies assume that removing nodes or links causes proportional structural failure. But let us consider the following hypothetical experiment where there is a network of interconnected sub-systems, and the functionality of the system as a whole depends on the exchange of information between modules A and B:
Surely, signalling needs less time through the central sub-system and more time through other pathways. Therefore, if the central sub-system is attacked (e.g., disconnected) then A and B will be unable to communicate as fast as before, but they will still operate with some delay for a given amount of time (e.g., until bottleneck or congestion effects will take place). So: structure can remain intact while functionality collapses within a time scale.
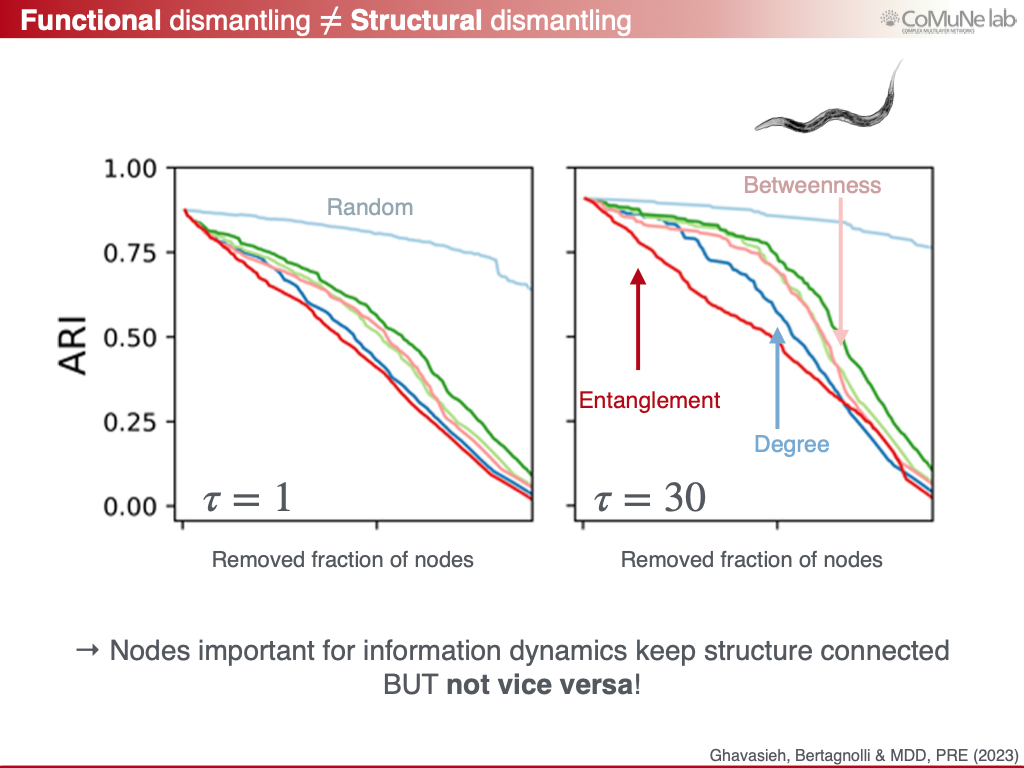
To quantify this, we developed Average Received Information (ARI) and entanglement centrality, which capture the ability of nodes to exchange information through the whole system and a node’s true contribution to information flow, respectively.
In the neural network of C. elegans, in the human connectome and in the Chilean power grid, entanglement-based attacks revealed vulnerabilities invisible to structural metrics. In short: robustness is not just about staying connected, but about sustaining functional pathways across time scales.
Emergence of Sparsity. Across biology, technology and society, networks tend toward sparsity: relatively few edges for many nodes. But why? Is there some fundamental principle to describe this emergent phenomenon?
We find that sparsity is the optimal balance between signaling speed and response diversity: too many links accelerate signaling but erase response heterogeneity; too few preserve diversity but slow coordination. By maximizing a utility function that weighs both (resembling the shape of a thermodynamic efficiency), the theory predicts a linear scaling between the number of edges and nodes in a network, matching empirical observations across nearly 600 networks from six domains. Sparsity, in this sense, emerges as thermodynamic law of organization.
Take home message
I think that functionality has been a missing dimension of network science, so far. By uniting principles from statistical physics, information theory and quantum mechanics, we can begin to predict — not just describe — how systems endure, adapt or fail, from first principles.
→ Please, remind that if you find value in #ComplexityThoughts, you might consider helping it grow by subscribing, or by sharing it with friends, colleagues or on social media. See also this post to learn more about this space.