Phantom oscillations in your data?
How dimensionality reduction using PCA can fool your results
If you find Complexity Thoughts interesting, follow us! Click on the Like button, leave a comment, repost on Substack or share this post. It is the only feedback I can have for this free service. The frequency and quality of this newsletter relies on social interactions. Thank you!
Dall-e 3 representation of this issue’s content
In the last weeks there were some rumors about the interpretation of principal component analysis (PCA) in specific contexts. In fact, as for any other mathematical tool, it could be misleading to blindly apply PCA and directly interpret its output without going deeper into details.
Introduction
When I was a MSc student working on my thesis, I had to analyze time series of the flow of ultra-high energy particles (UHECR) detected at the Pierre Auger Observatory, in Argentina. My goal was to model that flow, which exhibited features typical of stochastic processes (mostly as expected) and of deterministic systems (rather unexpected).
One of such features was a finite and low correlation dimension, a feature well known for characterizing deterministic dynamical systems. That was exciting at the very beginning: I was finding the signature of an unexpected deterministic component of the flow, even after correcting for daily and seasonal patterns. It was at that point that I had the great opportunity to get in touch with the great Antonello Provenzale, to better understand the phenomenon. At the end of the day, it turned out that one of the previous discoveries by Antonello was related to my curious results.
In fact, together with A. Osborne, Antonello demonstrated that “a simple class of “colored” random noises characterized by a power-law power spectrum have a finite and predictable value for the correlation dimension”. Why that’s important? Because it was contradicting the take (dominant in those days) that it was sufficient to detect a finite fractal dimension to have deterministic chaos. That paper is among the most cited ones in the literature of nonlinear time series analysis.
Using algorithms designed (or supposed) to work under specific assumptions might lead to misleading results. Thanks to Antonello my thesis went well anyway.
Going to the PCA
Let’s start from this paper:
Interpreting principal component analyses of spatial population genetic variation
Nearly 30 years ago, Cavalli-Sforza et al. pioneered the use of principal component analysis (PCA) in population genetics and used PCA to produce maps summarizing human genetic variation across continental regions1. They interpreted gradient and wave patterns in these maps as signatures of specific migration events1,2,3. These interpretations have been controversial4,5,6,7, but influential8, and the use of PCA has become widespread in analysis of population genetics data9,10,11,12,13. However, the behavior of PCA for genetic data showing continuous spatial variation, such as might exist within human continental groups, has been less well characterized. Here, we find that gradients and waves observed in Cavalli-Sforza et al.'s maps resemble sinusoidal mathematical artifacts that arise generally when PCA is applied to spatial data, implying that the patterns do not necessarily reflect specific migration events. Our findings aid interpretation of PCA results and suggest how PCA can help correct for continuous population structure in association studies.
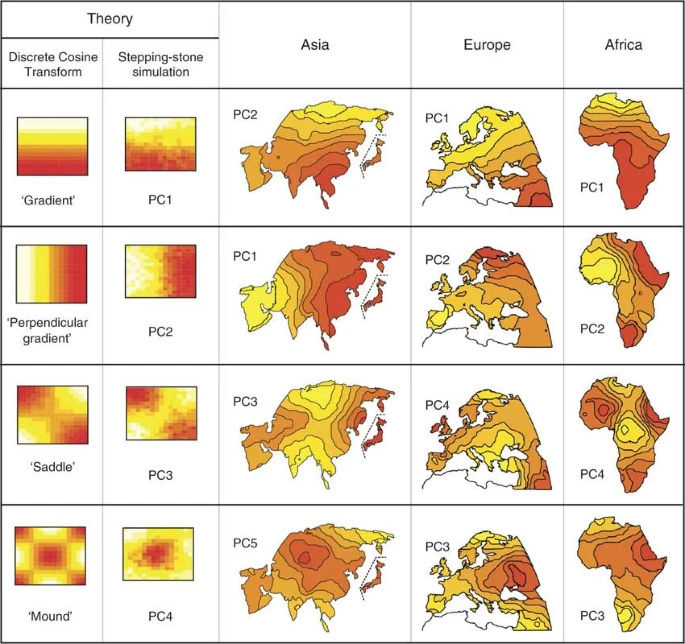
The first figure is crucial:
From the figure caption: “The first column shows the theoretical expected PC maps for a class of models in which genetic similarity decays with geographic distance (see text for details). The second column shows PC maps for population genetic data simulated with no range expansions, but constant homogeneous migration rate, in a two-dimensional habitat”.
In a nutshell? The interesting observed patterns can be explained by a simple model, simpler than the one used by Cavalli-Sforza et al in this paper, for instance. The meaning of the findings changes dramatically too.
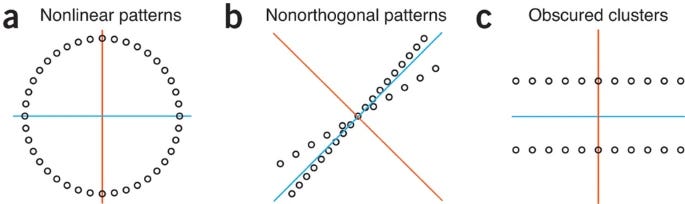
In fact, there are well known limitations to PCA (as well as for other dimensionality reduction techniques), as outlined here:
“As with all statistical methods, PCA can be misused. The scaling of variables can cause different PCA results, and it is very important that the scaling is not adjusted to match prior knowledge of the data. If different scalings are tried, they should be described. PCA is a tool for identifying the main axes of variance within a data set and allows for easy data exploration to understand the key variables in the data and spot outliers. Properly applied, it is one of the most powerful tools in the data analysis tool kit.”
Troubles for neuroscience data?
More recently, another paper has shown the potential issues in using PCA with neuroscience data:
Phantom oscillations in principal component analysis
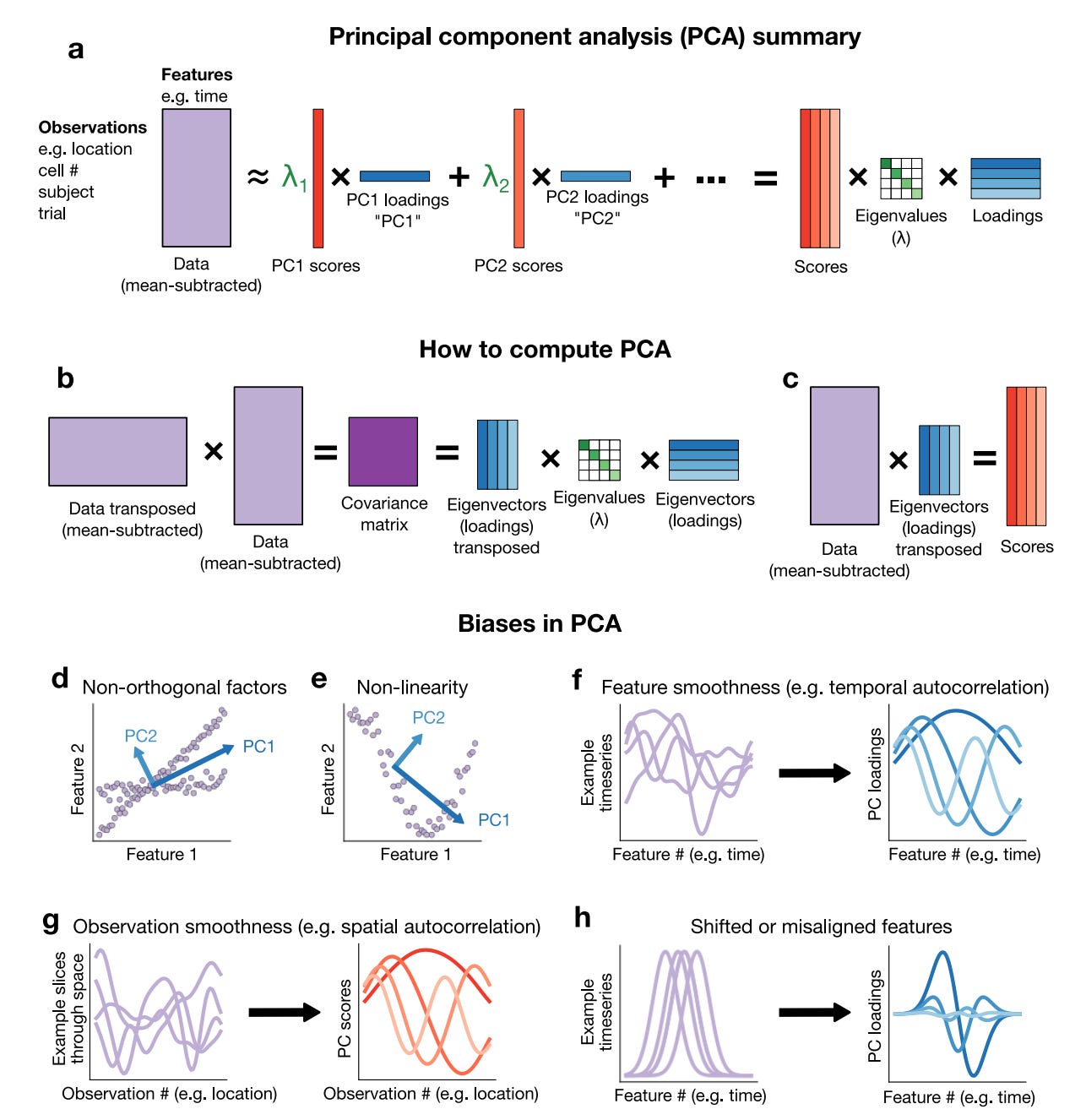
Dimensionality reduction simplifies high-dimensional data into a small number of representative patterns. One dimensionality reduction method, principal component analysis (PCA), often selects oscillatory or U-shaped patterns, even when such patterns do not exist in the data. These oscillatory patterns are a mathematical consequence of the way PCA is computed rather than a unique property of the data. We show how two common properties of high-dimensional data can be misinterpreted when visualized in a small number of dimensions.
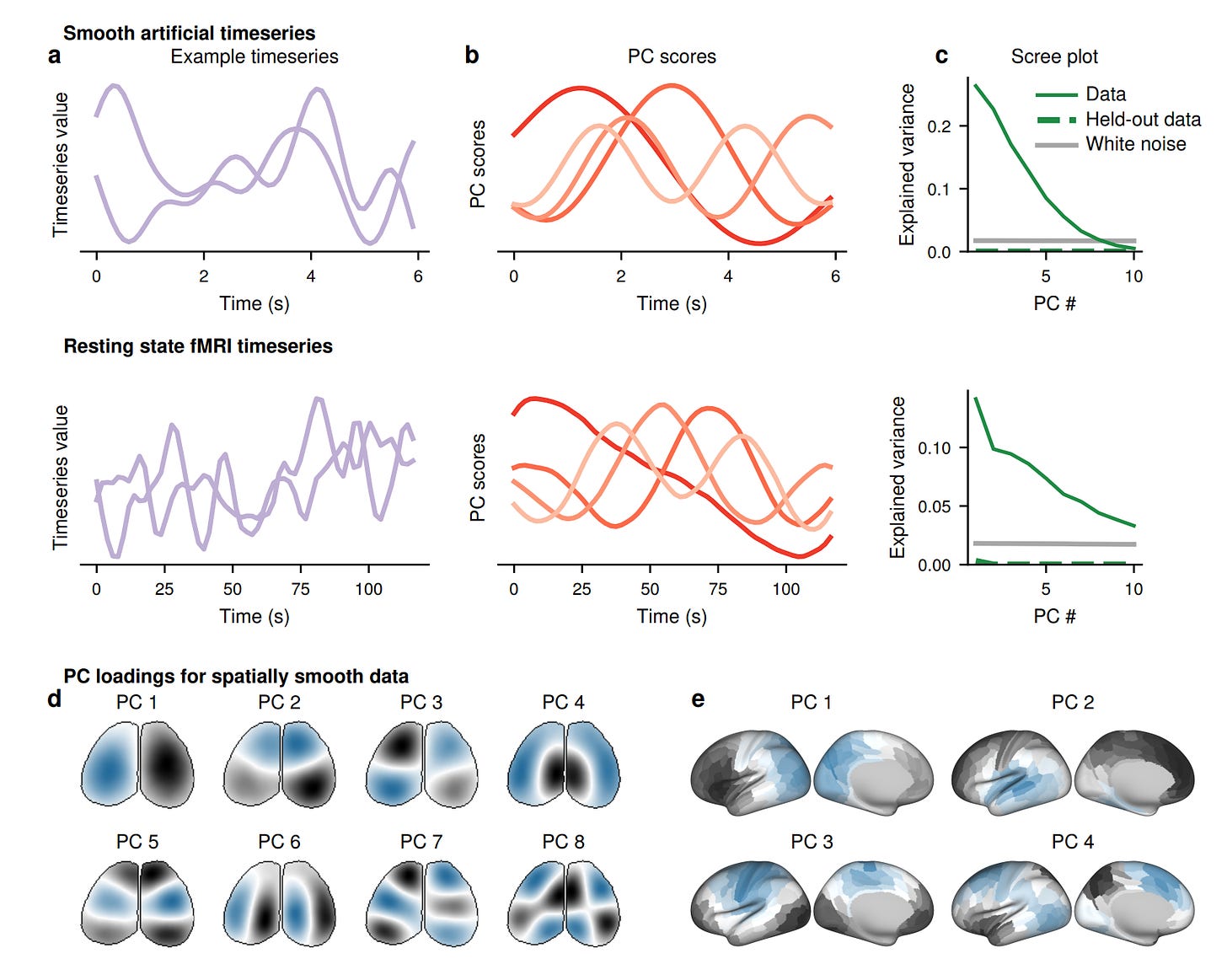
In fact, for (continuous) non-oscillatory data it is possible to detect oscillatory principal components! These behavior is due to smoothness and shifts in time or space, features of most (if not all) data analyzed in neuroscience, for instance.
Collectively, our work demonstrates that patterns which emerge from high-dimensional data analysis may not faithfully represent the underlying data
This is bad news for the ones using PCA, but it’s good to know when analyzing data falling outside the hypotheses/assumptions made by the PCA algorithm (and this is valid for any algorithm in general).
Figure: Source of biases in PCA, taken from here.
Why such “phantom oscillations” emerge? The answer could be easier than expected.
The author of the above paper, starts from the (generalized) continuous version of PCA, also known as the Karhunen-Loeve transform, which in turn relates to the Kosambi–Karhunen–Loève theorem stating that “a stochastic process can be represented as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function on a bounded interval”.
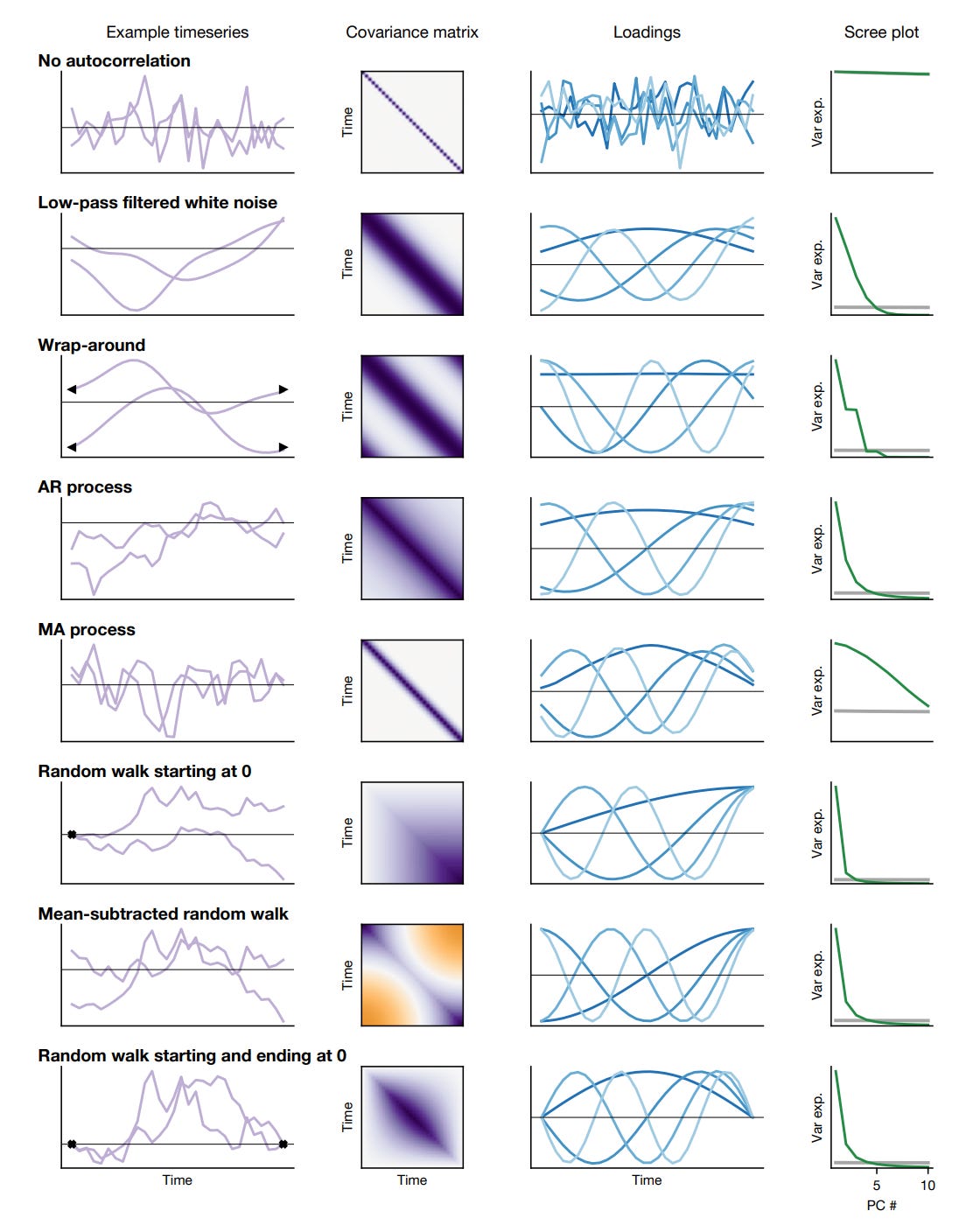
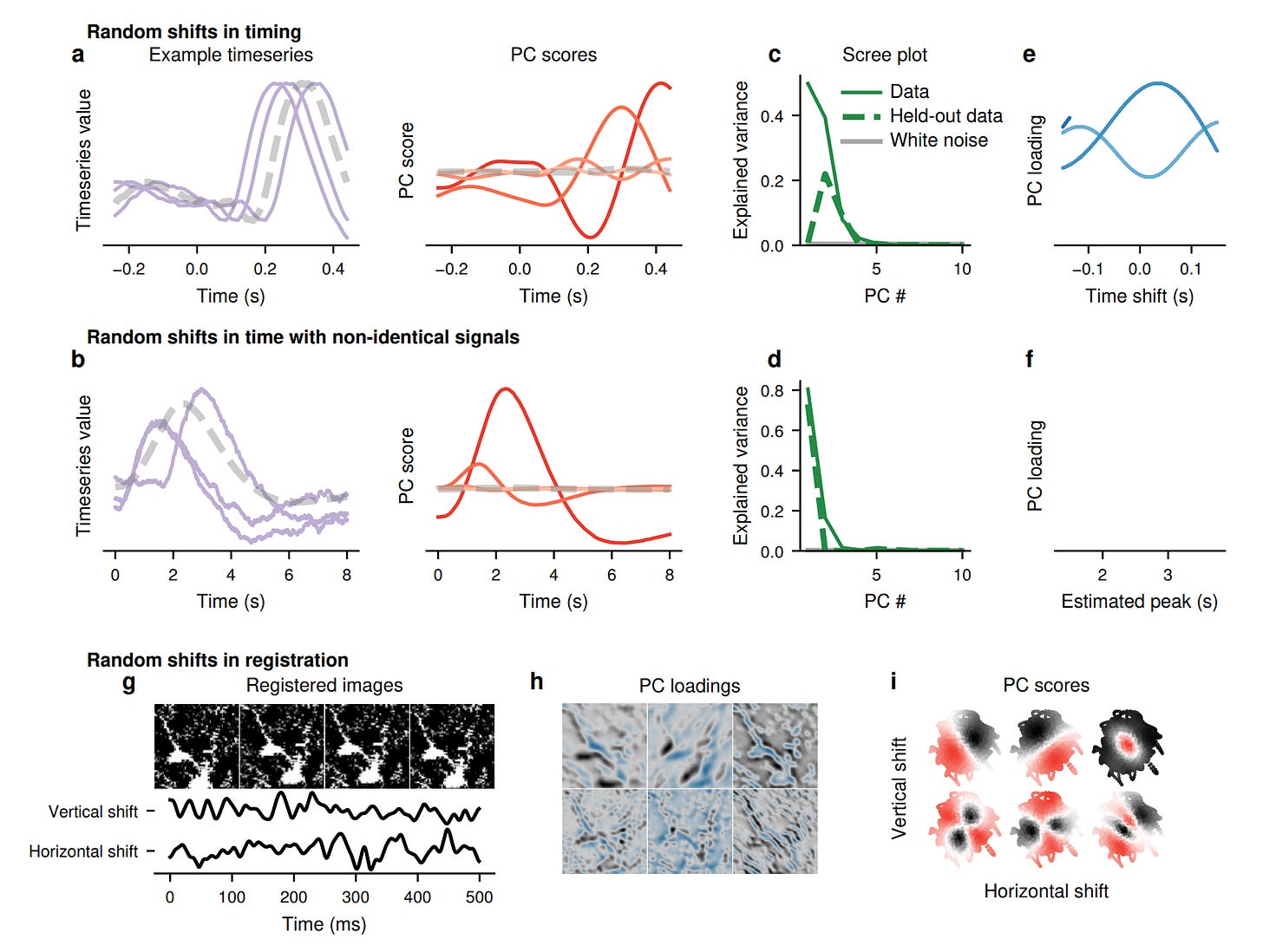
For specific processes such as the Brownian motion or the Ornstein-Uhlenbeck processes, it is possible to analytically show the appearance of phantom oscillations. It might sound crazy, but for a variety of stochastic processes you will find those phantom oscillations with peculiar PCA patterns, as shown in the figure below where different types of smoothness are considered:
What about brains? Here we go:
even in the case of time shifts:
Making sense of this fact in a nutshell
We can try to make sense of these results using some intuition and starting from a quote by Konrad Kording, who recently wrote on X/Twitter:
In a 1/f world, PCA = fourier
Short and easy. But why?
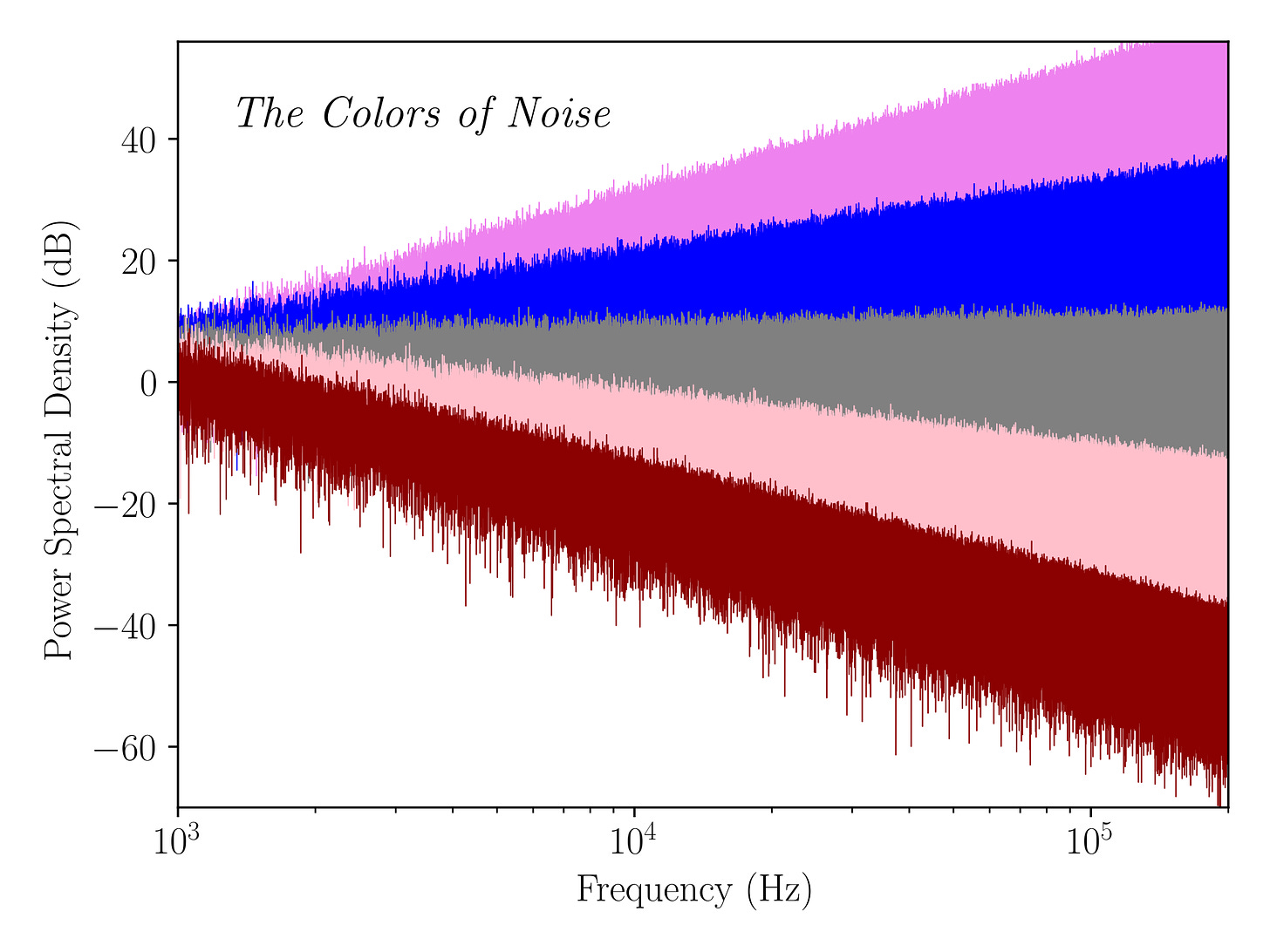
Well, the aforementioned stochastic processes can be imagined as special case of colored noise, since their power spectrum follows some scaling law in the frequency domain:
Figure from Wikipedia.
Let’s focus on a specific type of noise, usually referred to as 1/f (or pink noise) since its spectrum decays exactly with the inverse of the frequency. This implies that lower frequencies have higher power.
In parallel, PCA involves the diagonalization of the covariance matrix of our data, finding the eigenvectors and eigenvalues of the covariance matrix.
Since in 1/f noise lower frequencies dominate the power spectrum, the components of our dataset corresponding to these frequencies will have higher variances. In other words: the lower frequency components with higher power will dominate the covariance matrix.
The principal components (ie, the eigenvectors) corresponding to these dominant low-frequency components can exhibit oscillatory behavior because they are representing the primary variance-causing elements in the data, which are inherently oscillatory due to the nature of 1/f noise.
Take home message
When analyzing (nonlinear) data from a complex system, never trust the output of any algorithm (especially the ones designed for linear analysis under a set of assumptions) without investigating its behavior in controlled experiments.



Maybe you know, but someone on X suggested that the analysis in this paper are perhaps related to what you are talking about: https://doi.org/10.1140/epjds/s13688-016-0093-1 https://rdcu.be/dyn0A